Podstawową podstawą wszystkich nauk, które znają świat matematyka. Dokładne zastosowania naukowe sformalizowany język oraz bada porządek, strukturę i relacje na wybranych obiektach abstrakcyjnych. Nie wszyscy uczniowie lubią matematykę z tego powodu złożoność i zamieszanie, ale najprawdopodobniej dlatego nieporozumienie. Trwałe zmiany w matematyce będą wymagały poświęcenia, koncentracji, konsekwencji, a nawet uporu i, co najważniejsze, praktycznych rozwiązań. W badaniu ważne jest, aby krok po kroku zrozumieć najpierw proste i stopniowo przechodzić do bardziej złożonych, nie pozostawiając niczego niezrozumiałego i źle pomyślanego.
Istnieje wiele różnych gałęzi matematyki, które zostały wystarczająco przestudiowane i pojawiły się niedawno. Poniżej opisano podstawy analizy matematycznej - podstawowe pojęcia wstępne, definicje i zasady badania prostych funkcji jednej zmiennej, pochodnej i zróżnicowania.
Aforyzm powstał wśród uczniów szkół podstawowych: „Matematyka staje się naprawdę skomplikowana, gdy znikają z niej liczby”. Rzeczywiście, zbliżają się do zrozumienia niektórych definicji i praw nauk matematycznych, decydując o regułach na konkretnych przykładach..
Kluczowe definicje
Zacznijmy od terminologii - od prostych ogólnych znaczeń semantycznych podstawowych definicji:
- Zmienna - wartość lub symbol, może przyjmować dowolną liczbę wartości
określony obszar (waga lub wzrost dziecka)
- Funkcja - cel, praca, aktywność, określone działanie na zmiennej, oznaczamy f (x) (zależność wagi dziecka od jego wzrostu)
- Limit - granica, granica, krawędź (horyzont - pole widzenia)
- Pochodna - uformowane, wtórne, płynące z innego, oznaczamy f '(x) (prędkość podczas ruchu)
- Różnicowy - różnica, rozróżnienie, separacja.
Funkcja jest po prostu
Funkcja jest wynikiem tego, co robi ze zmienną, którą jest wynik obliczeń. Jest to relacja elementów, w której zmiana jednej zmiennej powoduje zmianę w innej. Podziel f (x) na proste i złożone.
Do wyświetlania zależności stosowane są następujące metody: algebraiczne, graficzne, tabelaryczne, logiczne, a nawet programowe.
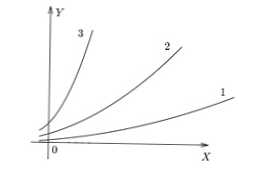
Zależności numeryczne są określane algebraicznie za pomocą symboli zmiennych, równości i nierówności (≤ i>), budowane jest równanie postaci: y = f (x), tutaj x jest zmienną lub argumentem, a y lub f (x) jest funkcją. Dla każdej konkretnej wartości zmiennej x z dopuszczalnej dziedziny definicji odpowiada pewna wartość y dla danego f (x).
Poniższy rysunek pokazuje proste wykresy 3 różnych proporcji. Można zauważyć, że w f (x) 3 największą wartość y uzyskuje się dla x swoistej, w f (x) 1 - najmniejszej.
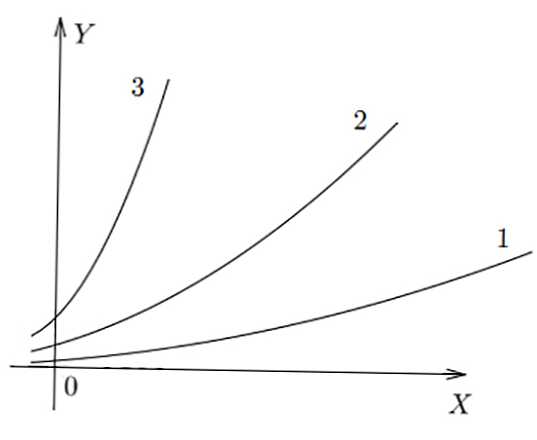
Funkcja
Wyróżnia się następujące wyrażenia elementarne: liniowe (bezpośrednie), kwadratowe (parabola), sześcienne, hiperbola, wykładnicze, logarytmiczne, trygonometryczne (przedstawione w poniższej tabeli).
Do analizy każdego typu f (x) określa się ich nieodłączne właściwości (wymienione poniżej); w tym celu stosuje się pojęcia pochodnej i różniczki.
Funkcja pochodna
Pochodna - operator, które dla pierwotnego f (x) zgodnie z prawami różnicowania kojarzy inną funkcję, w pewnym momencie charakteryzuje zmianę pierwotnego f (x) argumentu x. Aby uzyskać szczegółowe zrozumienie, należy zająć się bardziej złożonymi definicjami granicy zależności i zróżnicowania..
Limit - ta definicja jest dynamiczna. Wyrażenie, które x dąży do n, rozumie się następująco: x uzyskuje wartości, które są zbliżone do n i różnią się nieznacznie.
Różnicowy - niewielka zmiana jakiejś wielkości. Przyrost nazywa się deltą.
Pochodna dla f (x) w punkcie jest granicą dzielenia delty funkcji przez deltę zmiennej w danym punkcie, jeśli ta ostatnia ma tendencję do 0.
Charakterystykę szybkości zmiany zależności w danym punkcie, geometrycznie można to przedstawić jako wartość tan kąta nachylenia stycznej alfa do funkcji.
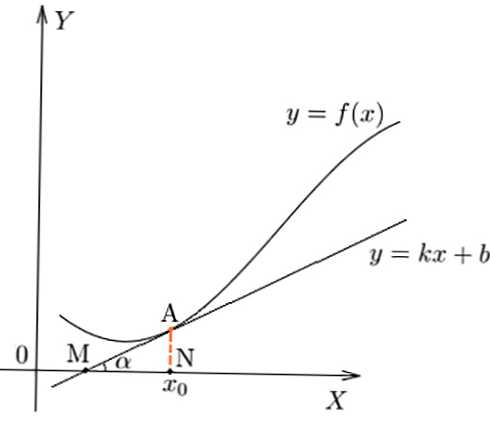
Pochodna
Zależność nazywa się różniczkowalną, jeśli zdefiniowano f '(x). Znalezienie pochodnej nazywa się różnicowaniem. Zasady obliczania f '(x) i dopasowania f' (x) z elementarnego f (x) podano w poniższej tabeli
Funkcja pochodna również działa
Każda zależność ma określone właściwości, znając je i badając je, możesz analizować naturę stanu i zmiany f (x).
Główne właściwości:
- Definicja i dane luki wartości.
- Zero f (x)
- Funkcja zwiększa się lub zmniejsza w niektórych odstępach czasu.
- Punkty funkcji MAX i MIN, czy jest fleksja.
- Parzyste lub nieparzyste f (x)
- Ograniczona i nieograniczona funkcja.
- Czy są jakieś asymptoty?.
- Częstotliwość f (x).

Funkcje i pochodne
Przy ustalaniu charakterystyk zależności za pomocą pochodnej stosowane są wzajemne połączenia właściwości f '(x) z właściwościami f (x) i odwrotnie. Charakterystyki f '(x) można łatwo określić na wykresie funkcji i odwrotnie, charakterystyki pierwotnej f (x) są rozumiane na podstawie wykresu f' (x). Naprawiając istotę każdej cechy funkcji, zbadaj i ustal łańcuch relacji. Aby określić asymptoty na wykresach, stosuje się pojęcie granic..
Poniżej przedstawiono niektóre cechy i zależności f '(x) od f (x):
- Gdy f (x) rośnie w przedziale, f '(x) jest dodatnie.
- Jeśli f (x) zmniejsza się w tym przedziale, f '(x) jest ujemne.
- W obecności f (x) punkt MAX, f '(x) = 0 w nim nie może być określony, a tg kąta stycznej zmienia znak od + do -.
- W obecności f (x) punkt MIN, f '(x) = 0 w nim nie może być określony, a tg kąta zmiany stycznej znak od - do +.
- Podczas gięcia f (x) w E wartość f '(x) nie zmieniała znaku w punkcie, f' (x) = 0.
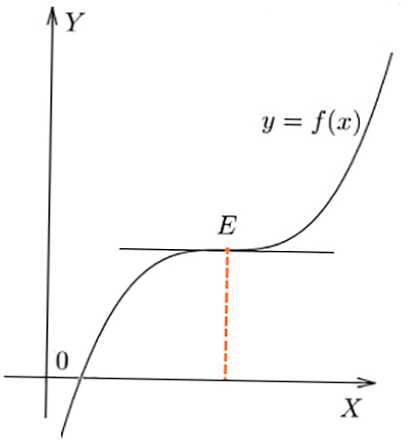
Zanieczyszczenie w punkcie E wykresu funkcji
Do celów badań f (x) tworzy schemat, w którym każdy etap jest konstruowany zgodnie ze specyficznym algorytmem do obliczania i analizy związków elementów składowych.
Różnice w funkcji i pochodnej
Reguły dodawania i odejmowania f (x) są takie same jak reguły tych akcji podczas różnicowania. Ale zasady znajdowania f '(x) pod działaniami mnożenia i dzielenia funkcji są różne (jak w tabeli).
Funkcja jest pierwotna, a pochodna jest wtórną operacją matematyczną; w większości przypadków mają one różne cechy.
Punkt przegięcia ciągłej zależności znajduje się przy jego drugiej pochodnej, jego znak powinien się zmienić w obszarze punktu x0.
Istnieją takie typy funkcji, które nie mają f '(x) w punkcie x0 (nieciągłe). W wyrazie ln (| x | -1) pochodna nie jest zdefiniowana w punkcie x0 = 1.
Istnieją wyrażenia „modulo” podobny do y = | x |, który ma załamanie w x0.
W przypadku takich zależności stosuje się tylko częściowo (w przedziałach dziedziny definicji) metody badania ich właściwości za pomocą pochodnych i nie zawsze jest możliwe przejście z właściwości f '(x) na właściwości pierwotne.
Nigdzie nie można się obejść bez wyjątków od zasad, a nawet w matematyce. Aby przeanalizować i utrwalić prezentowany materiał, konieczne jest rozwiązywanie przykładów, ćwiczenie, zdobywanie doświadczenia z limitami, różnicami i pochodnymi oraz odważne przejście do całek.











